|

Laboratory
Optical Work
Source:
Procedures in Experimental Physics
by John
Strong
Introduction.
In this chapter we will describe the technique of making the optical surfaces
required for mirrors, prisms, interferometers, lenses, and so forth. The
optical surfaces on these instruments are characterized by being much
more accurate than ordinary machined and ground surfaces. In fact, optical
tests sensitive to a few millionths of an inch are necessary to show their
lack of true perfection. Since our concern here is with high-precision
work, in which errors are usually less than a wave length of light, we
do not include methods used for plate glass, cheap lenses, and other commercial
work in which the tolerance is greater.
The technique described
here is intended primarily to guide the research worker who finds it desirable
or necessary to prepare his own optical surfaces.
In any case the task
set before the worker is that of generating an extremely accurate polished
surface. Accordingly, we will first set down the general technique involved
without detailed reference to what is being made. Later we will treat
of special procedures.
General procedure.
The glass or other material on which the optical surface is to be prepared
is first roughly formed to the desired shape. For example, in the case
of a lens, the first step will consist of cutting out a disk of glass.
A prism will be first sawed or ground to rough dimensions from a larger
block. The proposed surface itself is then generated more precisely by
periods of grinding with suitable laps. The surface is ground first with
coarse grits of Carborundum to conform approximately to the specifications.
Then finer and finer abrasives are used until at last the grinding is
terminated with the finest emery flour. The grinding is periodically interrupted
for testing with a straightedge, template, micrometer, or spherometer.
After fine grinding, the surface is polished with a pitch lap and rouge.
Finally it is brought as near to perfection as the specifications require
by "figuring," that is, by local retouching with polishing tools. The
figuring is guided by delicate optical tests.
Theory of grinding
and polishing. Optical grinding and polishing are alike in that both
require the use of a material which is harder than the glass. This material
is used in the form of loose grits or fine powder. The two operations
are unlike in that the grits and powder used for grinding are worked over
the surface with a hard tool, ordinarily made either of glass or cast
iron, whereas polishing tools are made from a soft base material. A polishing
tool for preparing precise optical surfaces is usually composed of some
combination of pitch and wax as the soft base material. Paper cloth and
wood are often used for polishing tools in cases in which no great precision
is demanded.

Fig. 1. |
The grinding process
depends upon the characteristic conchoidal fracture produced when an excessively
high pressure is applied to a point in the surface of the glass. The pressure
exerted on the surface by a single particle of abrasive or grit, as it
is rolled about between the tool and the work, builds up stress beyond
the strength of the glass, resulting in the removal of a chip. This is
illustrated by Fig. 1. Carborundum and emery grits are ordinarily used.
The efficiency of the process depends primarily on the sharpness of the
grits. Carborundum grits break down faster than emery, although they are
harder than emery. Fractured Carborundum grits have sharp edges and consequently
they grind fast. Ellison1 says that Carborundum grinds about
six times as fast as emery. Carborundum is used for the first coarser
grades of grits, and emery for the last finer grades. Natural emery (corundum)
cuts about twice as fast as synthetic emery. The corundum produces a smoother
surface than either Carborundum or synthetic emery and is, accordingly,
best for the final grinding.
The hardness of various
abrasives is indicated in Moh's extended hardness scale. (See Table I.)
 |
From a practical
point of view, we may consider that the polishing operation is a planing
process.2 The grains of abrasive appear to fix themselves automatically
in the soft material of the tool, usually pitch, so that their crystal
surfaces are parallel to the direction of motion of the tool and parallel
to the plane of its surface. Thus a complex scraper is formed. As this
moves over the glass, the height of each abrasive particle is automatically
adjusted in the soft backing so that it produces a fine smooth cut. The
removed glass is washed away by the liquid lubricant, usually water. The
planing action starts on the peaks of the "hills" that result from the
fine grinding and produces a full polish there at the first stroke. Continued
operation of the polishing tool removes additional glass, so that the
hills become plateaus and are finally planed down to the level of the
deepest valleys. The character of the surface on any particular plateau
is not improved by continued polishing–it is to be regarded as fully
polished from the first stroke. This is illustrated in Fig. 2. After the
whole surface becomes uniformly polished, further working with the polishing
tool removes additional glass. In constructing an experimental aspheric
camera lens, as much as thirty thousandths of an inch of glass has been
removed by polishing.

Fig. 2. |
Methods of polishing.
Glass can be successfully polished with almost any fine abrasive, provided
a suitable soft and yielding backing is used. For some types of work–for
example, for edging mirrors where irregularities in the surface do not
matter–glass is polished with a wood tool charged with Carborundum
or emery. Glass may be polished with rouge, either the red oxide or the
magnetic black oxide, and also with charcoal or oxide of tin. However,
for ordinary optical work rouge is the most satisfactory polishing material.
Surfaces of glass, quartz, speculum metal, calcite, and fluorite are best
polished with rouge on a wax or pitch tool. The action of various polishing
agents depends on the type of backing, whether cloth, paper, or pitch
is used, on the hardness of the material being polished, and on the method
of lubrication. Some agents which are indifferent polishers when used
with a wax or pitch tool and lubricated with water are quite effective
when used dry on a paper lap. For paper polishing, oxide of tin (putty
powder) is commonly used. Chromium oxide ( )
is recommended for polishing certain metals such as stainless steel which
are "attacked" by rouge. )
is recommended for polishing certain metals such as stainless steel which
are "attacked" by rouge.

Fig.
3. |
The material for
the polishing tool may be a soft metal– copper, lead, or aluminum.
Tools made of these metals are sometimes used for polishing thin specimens
of minerals which are to be examined with the microscope. Levigated alumina
is usually employed as abrasive for work of this type.
The polishing tools
used in precision optical work are made of pitch or pitch and wax compounds,
in contrast with cloth or paper-faced tools used on some commercial products.
Glass is polished with surprising rapidity on a cloth polisher, but it
exhibits a peculiar grainy "lemon-peel" surface. This method of polishing
is generally used in the manufacture of plate glass. Paper polishers in
general produce a somewhat better surface than cloth but are seldom used
except for the manufacture of inexpensive lenses, such as for cheap hand
magnifiers and so forth. All polishing tools of a fibrous nature produce
a "lemon-peel" surface.
Procedure for
optical surfaces of 3 to 6 inches in diameter and larger. The technique
which will form the nucleus of our first treatment is particularly suited
to the making of surfaces of 3 to 6 inches in diameter or larger worked
in glass or quartz. The procedures involved are fundamental and apply
equally to mirrors, lenses, or prisms. The method treated here is used
by D. O. Hendrix, a practicing optician associated with Mount Wilson Observatory.3
This procedure is different in some respects from that described in the
classic book on amateur telescope making by Ingalls, Porter, and Ellison.4
For example, in their book they recommend using the tool underneath the
work, while here we treat primarily of the method using the tool on top
of the work.

Fig. 4. |
Cutting and roughing
out the work. The work, whether it is a mirror, a lens, or a prism,
can often be cut to rough shape from stock plate glass with an ordinary
wheel cutter, the most common form of glass cutter, which is used for
cutting all kinds of polished glass in all ordinary thicknesses. The cutter
is drawn across the glass surface once with sufficient pressure definitely
to mark the glass. It should not be run back and forth along the same
line. After the glass is "marked," it is broken by bending it away from
the cut, as shown, for example, in Fig. 3. The parallel-jawed pliers,
also illustrated in Fig. 3, are useful for making narrow cuts. The break
may also be started by lightly tapping the glass on the back side opposite
the mark with the small knob provided on the handle of the wheel cutter.

Fig.
5. |
The procedure for
cutting thick plate glass is to lubricate the wheel cutter with turpentine
or kerosene before the cut is made. After the glass is marked, the break
is started with a blunt chisel. The chisel is held firmly against the
back of the glass at a point directly opposite the mark and tapped sharply
with a small hammer. The edge of the chisel should be parallel to the
mark. It is well to have the glass supported, cutter-mark down, on a cloth
or padded surface. When the break has started, it is led along the cut
with the chisel.
Very thin glass is
best cut with a diamond point especially mounted and sharpened for this
purpose.5

Fig. 6. |
If a disk is desired,
the glass is first cut square, and the corners are then cut to give a
polygonal piece approximating the desired shape. The rough edges may be
removed by holding the glass against a rotating flat disk of cast iron
fed with a mixture of Carborundum and water. (See Fig. 5.) Also, the glass
disk may be waxed onto a metal plate mounted in the headstock of a lathe.
As it is rotated, the edges are ground with an iron tool, which is fed,
with Carborundum and water as shown in Fig. 6 A light springy tool is
recommended. Oilcloth should be used to protect the lathe so that abrasive
does not get into its working parts or on its ways.

Fig.
7. |
Biscuit cutter.
A common method of cutting small disks (up to about 6 inches in diameter)
from slabs of glass is by means of a "biscuit cutter," This is simply
a thin-walled tube of iron or brass mounted in a drill press as shown
in Fig. 7. The rotating tube is fed against the glass, Carborundum and
water being applied with a spoon. Fig. 7 also shows a novel method of
central feeding. To prevent chipping when the biscuit cutter goes through
the glass, it is well to wax an auxiliary backing plate onto it with beeswax.
Grade 60 or 90 Carborundum should be used except for fine cuts or cuts
on delicate and fine work, in which case grade 120 Carborundum should
be used. The cutter will cut more rapidly if instead of water a mixture
of turpentine and camphor is used with the Carborundum. The proportions
of the mixture should be 5 grams camphor to 1/2 liter turpentine.

Fig. 8. |
Diagonal mirrors,
such as the Newtonian diagonal for a small telescope, may be cut out of
a larger figured flat mirror with the biscuit cutter. The larger mirror
is mounted in the drill press at an angle of 45 and cemented with beeswax on a backing of plate glass. It is cut in the
manner shown in Fig. 8. Usually the front of the flat is also coated with
a cover glass, stuck on with beeswax, to prevent scratching the figured
surface with the abrasive. A mirror thus cut out may develop a slight
turned-up edge. However, if the cut rim, which now has a rough ground
surface, is polished with wood and Carborundum, the figure of the mirror
will usually become flat again. (This is sometimes called the Twyman phenomenon.)
and cemented with beeswax on a backing of plate glass. It is cut in the
manner shown in Fig. 8. Usually the front of the flat is also coated with
a cover glass, stuck on with beeswax, to prevent scratching the figured
surface with the abrasive. A mirror thus cut out may develop a slight
turned-up edge. However, if the cut rim, which now has a rough ground
surface, is polished with wood and Carborundum, the figure of the mirror
will usually become flat again. (This is sometimes called the Twyman phenomenon.)

Fig. 9. |
Glass saws.
Strips and slabs of glass are cut from a thick piece of glass stock with
saws. The simplest and easiest of these to set up is the so-called "mud
saw," shown in Fig. 9(a). It consists of a rotating disk of soft sheet
iron fed with a mixture of Carborundum and water. Sometimes sugar, syrup,
talc, glycerin, or bentonite (particularly good) is added to this mixture
to make the Carborundum adhere to the blade and to keep the grits from
settling out in the reservoir pan. The usual construction allows one edge
of the saw to dip into the "mud," or Carborundum mixture, which is held
in a pan below the disk. The work to be slabbed is supported on a counterbalanced
table and is held against the saw with a slight pressure.
A diamond saw forms
an efficient slabbing cutter. The diamond saw shown at the bottom of Fig.
9 may be made as follows: The diamonds are pulverized as shown at (b)
and charged into the nicks of a circular disk prepared as shown at (c).
These nicks are rolled as shown at (d) to hold the diamond powder and
give the saw clearance. In operation the saw blade is lubricated and washed
with water or kerosene.
Modified Draper
machine. Once the prism, lens, mirror, or other blank is cut out,
the operations involved in grinding the curves and polishing and figuring
them may be carried out either by hand or with a grinding and polishing
machine. A machine like the one shown in Fig. 10, a so-called modified
Draper machine, is suitable.

Fig. 10. Note
that the universal joint shown here is used only for the rough grinding.
For fine grinding and polishing, the tool is connected to the crossarm
by a pivot and socket arrangement. See Figs. 16 to 20. |
The tool is moved
laterally by the modified Draper machine in a thin oval stroke across
the face of the work. The amplitude of this stroke is controlled by adjustment
of the throw of the crank. The stroke can be arranged by movement of an
adjustable guide so that it is either diametral or chordal in respect
to the work. The tool may be allowed to rotate freely, or it may be driven
by a belt. Also, the tool may be loaded to increase its pressure, or it
may be counterbalanced to decrease its pressure on the work. The table
on which the work is mounted is power driven to rotate about 2 r.p.m.
Support of the
work. It is very important to support the work properly, or it will
develop astigmatism, the anathema of optical work.
The first requisite
is to have the modified Draper machine table turned and lapped 0.001 to
0.003 inch concave, depending on the size. It is then covered with a layer
of thin felt and oilcloth as shown at the bottom of Fig. 10. This supports
the glass uniformly on its flat bottom side and effectively prevents flexure
during all of the operations. When the second surface of a lens is being
worked, the plane concave glass tool that was used in the fine grinding
of the first face is used to support the work on the grinding table. The
tool is first mounted on the table concave side up. Then it is covered
with felt and the lens is laid on it.

Fig.
11. Many workers will prefer to have the work at a lower level,
3 to 4 feet, than is shown here. Note: The operator shown in this
figure is left-handed |
The work is supported
laterally on the table by three edge arcs, which should fit neatly to
the edge of the blank without exerting any pressure on it except as is
necessary to balance lateral forces produced by the action of the tool.
The work is moved around in the edge supports from time to time during
grinding and polishing to distribute the effect of these forces uniformly
around the periphery of the mirror, to avoid the introduction of astigmatism.
The work, if it is
a mirror or lens, is prepared by having its face and back fine-ground
and made parallel with a rotating cast-iron lap used with loose grits
as shown in Fig. 5.
The edges are then
ground round and lightly beveled. Finally, the edges are polished with
a wood tool and fine Carborundum grains.
Grinding the curve
in the work. Full-size grinding tools of tough metal such as copper,
brass, or soft iron, when turned to a definite radius of curvature, will
reproduce this radius in the glass. The soft metal surface becomes charged
with abrasive and is not worn appreciably when it is used on a brittle
material such as glass. On the other hand, cast-iron tools change slowly
during grinding, and glass tools change at approximately the same rate
as the work.
The traditional way
of making a 6-inch mirror by hand is to use two equal disks of glass,
one as the work and the other as a grinding tool. The grinding is accomplished
as shown in Fig. 11 with the work mounted on a firm pedestal, the height
of which is optional. The optician walks around it as he strokes the work
with the tool. Pressure is applied to the center of the tool with the
thumb of the right hand. The tool is rotated with the fingers in a counterclockwise
direction as it is stroked across the right side of the work. When a chordal
stroke is used, the upper disk becomes concave and the lower convex. By
this means a certain amount of control is given the operator. He may continue
grinding, increasing the curvature in the surfaces all the time, until
the desired result is attained. If he wishes to decrease the curvature,
he will place the tool below and stroke it with the work. Or he may periodically
reverse the relative positions of the two disks if he wishes to hold the
surfaces fairly flat or constant in radius of curvature. When it is desired
to hold the curvature constant, a diametral rather than a chordal stroke
is used.
On the modified Draper
machine, the grinding of a mirror to a definite radius of curvature is
effected with a small tool. Concave curves are cut in the glass with a
1/3-size tool stroking the work across its center. A convex curvature
is generated by a sub-diameter tool stroked across a chord of the work.
Although a convex curvature will be generated if a full-size tool is stroked
across the center of the work (diametral stroke), it becomes convex more
rapidly when a chordal stroke is used. The rate at which the curvature
changes is proportional to the amplitude of the diametral stroke or the
offset of the chordal stroke.
After the work has
been roughed out to the proper radius of curvature with 90, or for extreme
curves 60, Carborundum the full-size tool is used to true up the surface.
The stroke used here is a thin oval across the center of the work. The
amplitude used is about one third to one sixth the diameter of the work.
The grinding is continued with the full-size tool until the tool and work
are spherical. This is indicated by the quality of the fit between the
tool and the work, which can be tested with a pencil mark made on the
work. This procedure may produce scratches. A circular template is often
made of the required radius and the work is ground until it fits this
template. Spherometers are also used to test the work for sphericity.
When the work is spherical, the spherometer reading, d, the radius
of curvature of the work, R, and the radius of the circle containing
the spherometer legs, r, are related as follows:
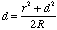
The spherical surfaces
obtainable by grinding are so good, in fact, that opticians who worked
before testing methods were developed as they are today hesitated to polish
the grinding pits entirely away, since they formed a convenient "landmark"
to which to refer the figure.

Fig. 12. |
To grind deep curves
like those required for an f/1 Schmidt camera, one puts a band
around the edge of the mirror and covers its face with a layer of Carborundum
grits. The band holds the grits on the mirror. As the work slowly rotates,
a fast lotating sub-diameter cast-iron ring tool is reciprocated diametrically,
or nearly so, across its surface in a thin oval stroke. The amplitude
of the stroke is adjusted so that the ring tool comes to the edge of the
work at the extremes of the stroke.
Final grinding in
all cases should be carried out with a glass grinding tool. Glass is used
rather than metal in order to have the tool change at approximately the
same rate as the work, thus insuring a more perfect fit at all times between
the tool and the work. The tool may be a glass disk formed as a complement
of the work; that is, if the work is a convex spherical surface of radius
R, the tool will be a concave sphere of almost exactly the same radius.
Or the tool may be a plate of glass cemented to a metal backing. It is
well to cut the grinding tool with one or more decentered grooves as shown
in Fig. 12 in order to prevent suction, facilitate the access of grinding
compound to all parts of the tool, and insure that the tool grinds slightly
faster than the work. These grooves may be cut into the glass with the
diamond or mud saw.
For large mirrors,
glass disks or squares can be cemented to a convex or concave iron backing
as is illustrated in Fig. 12.
The radius of curvature
of the work, R, is determined by means of a spherometer or more
simply by a template cut from metal. The latter can be cut with a sharp
steel point (sharpened like a brass turning tool) mounted on the end of
a board of length R and pivoted at the other end on a nail. For
flats a good straightedge may be used as a template.
Fine grinding.
After the proper radius is attained and the work has been trued up with
the full-size tool, the optician passes successively to grades 150, F,
400, and 600 Carborundum. The full-size tool, loaded to a pressure of
about 0.5 lb./square inch, is used. For a 6-inch mirror about a teaspoonful
of grits is applied at a time. Each application of grits, applied with
one or two spoonfuls of water, is allowed to grind until the gritty cutting
sound, which is heard at first, has softened. For a 6-inch mirror, grits
are repeatedly added until the work has been ground a total time of 30
minutes (or 1 hour by hand). After a half-hour of grinding with one grade
of Carborundum, the optician passes on to the next grade, and finally,
after the 600 grade Carborundum, finishes with two grades of emery, 302-1/2
and 303-1/2. The work, the table of the machine, and the tool should be
thoroughly washed after finishing with each grade of abrasive.
Carborundum grits
as obtained commercially are well graded and do not need to be washed.
However, the emeries must be washed each time they are used. The washing
procedure is as follows: Put emery to a depth of 1 inch in a quart Mason
jar, fill the jar with water, stir, and let settle for 10 seconds. Decant
the suspended emery off to a second clean jar and discard the residue.
After 10 seconds in the second jar, decant again, and repeat the operation
a third time. After this, the settling time is increased to a minute to
yield a residue which we will designate as residue A. The liquid
over this is decanted into a clean jar, in which it is allowed to settle
until it is clear, yielding residue B. The liquid over B
is then put back over residue A, stirred, allowed to stand for
1 minute, and then added again to B. This is repeated several times
to transfer a large fraction of the emery from A into B.
Residue B, when mixed with an equal volume of powdered washed talc,
is ready to be used for grinding. The talc serves as a lubricant and prevents
sticking of the tool. The talc must be washed in the same manner as the
emery was washed to free it of metallic iron.
The final grinding
with the two grades of emery will yield a surface which exhibits specular
reflection of white light at grazing incidence. At a steeper angle the
reflected image is red. In fact, specular reflection of the red part of
the spectrum up to a grazing angle of about 12 may be obtained. The maximum grazing angle of specular reflection affords
a simple test of the quality of the fine-ground surface. A clear filament
lamp should be used as a light source for this test, and when the surface
gives a reflection at a grazing angle of about 12
may be obtained. The maximum grazing angle of specular reflection affords
a simple test of the quality of the fine-ground surface. A clear filament
lamp should be used as a light source for this test, and when the surface
gives a reflection at a grazing angle of about 12 ,
the work is ready to be polished. ,
the work is ready to be polished.
When it is required
to have the center of the mirror perforated, the necessary hole is usually
cut with the "biscuit cutter" before the grinding is started. The plug
is then fastened back in place with plaster of Paris. The plug is left
in place until the figuring is finished.
Pitch for tools.
Polishing pitch should have the following properties: It should flow slightly
at ordinary room temperature; it should trim easily with a sharp knife;
and, further, it should not lose its "temper" by evaporation of volatile
oils. A compound which conforms to these specifications quite well is
made up as follows:
Coal tar (melting
point 170 to 180 to 180 F.)..... 2 Ibs.
F.)..... 2 Ibs.
Pine tar (Mefford
Chemical Company)..... 4 liquid oz.
Beeswax .....12
oz.
Venioe turpentine .....not
more than about 2 or 3 cc.
The tar is melted
and the other ingredients are added in the order listed.

Fig.
13. |
The function of the
turpentine is to adjust the final "temper" of the pitch. More or less
turpentine is added, depending on whether a hard or soft pitch is desired.
Before adding the turpentine and after each addition, test the pitch for
temper. The simple method of performing this test is to chew a small sample
of the pitch after chilling it by pouring it out on a cold glass surface.
At body temperature, so-called "soft" pitch can be chewed, while "hard"
pitch cracks under the pressure of the teeth. Furthermore, hard-pitch
tools stored face up will show evidence of flow in the sides of the groove
in about a week. A soft tool exhibits flow after standing a day. Polishing
pitch does not attain its final hardness on cooling but continues to harden
for a day or more. This is a sort of "jelling" process, which must be
taken into account.
After the correct
mixing temper is attained, pitch is filtered to remove small sticks or
other hard particles. The hot pitch is poured through a cheesecloth filter
supported or, an iron ring. Two layers of cheesecloth are adequate to
hold back harmful impurities.

Fig. 14.
|
Polishing tools of
6 inches in diameter or less are made by simply pouring the melted pitch
compound over a support to a depth of about 3/8 inch. After the pitch
has cooled, it is channeled by cutting it with a hot knife so that the
surface is divided into a decentered system of square facets of uniform
size. These facets are later trimmed in the manner shown in Fig. 13. Tools
having bubbles in the pitch cause no trouble unless it happens that the
bubbles occur in a definite zone on a full-size tool that is to be worked
over the mirror or lens with a short stroke. In order to avoid a zone
of bubbles, the pitch is cast by pouring it onto the support at one edge
rather than at the center.
There are two methods
of accommodating the tools to the different working conditions of summer
and winter: By one, the formula is changed, the pitch being tempered with
more turpentine for cooler weather; by the other, the size of the facets
is changed. The facets are made smaller in cooler weather. When the formula
given above is used, the facets should be about 1 inch square for temperatures
above 75 F. and about a 1/2
to 3/4 inch square for temperatures below 75 F. and about a 1/2
to 3/4 inch square for temperatures below 75 F.
F.
If the polisher is
to be used on soft or easily scratched material, such as speculum metal,
it is advisable to use harder pitch and to have the facets narrow. The
channels allow the pitch to flow evenly and also allow the rouge and water
free access to all parts of the work. For speculum metal it is recommended
that the facets be 1/32 to 1/16 inch wide and 3/4 inch long.

Fig.
15. |
To construct a polishing
tool of relatively short radius, the pitch facets are first cast in a
suitable mold in the form of sticks. (See Fig. 14.) These are then cut
into squares and fastened to the metal tool as shown in Fig. 15.
After the tool has
been faceted, it is warmed and pressed to the work, with soap in a 25
per cent glycerin solution as a lubricant on the work to prevent sticking.
The pressing operation is illustrated in Fig. 16. The tool is gently warmed
over a hot plate until the pitch is soft. Then it is applied to the work,
wet with a mixture of soap and glycerin, and left to cool. This procedure
yields an intimate contact between the tool and the work. Tools for flats
may be first turned in the lathe before they are pressed. After pressing
the pitch tool, it is advisable to wash it in cold water and also wash
and dry the work to remove the soap and glycerin.

Fig. 16.
|
Polishing.
Polishing is carried out on the table of the modified Draper machine in
the same manner as grinding, except that the polishing tool is usually
allowed free rotation. Rouge and water is added to the work from time
to time near the edge of the tool with an eye dropper. The rouge should
be washed. The washing procedure is the same as that described for washing
emery or talc, except that the settling time is longer–up to one-half
hour.
Hard facets in the
tool may cause sharp zones to appear in the work during polishing. To
avoid the effects of such surface inhomogeneities in the pitch and resultant
irregularities in the cutting action of the tool, the work is "broken
up"; that is, the tool is frequently (and irregularly) given a spin. The
facets in the tool should form a decentered system. A diametral stroke
is employed for polishing. A feature of the polishing machine which also
contributes to breaking up the work is the incommensurable coupling obtained
by the belt which connects the rotation of the work with the phase of
the stroke. The stroke is varied from time to time from a long stroke
of one fourth the diameter of the tool to a short stroke.
If the surface of
a pitch polishing tool becomes so heavily charged with rouge that it appears
hard and glassy, the polishing speed will be considerably reduced, and
furthermore "sleeks" are liable to appear. Sleeking, or the appearance
of groovelike marks on the polished surface, is probably caused by the
formation of ball-shaped aggregates of rouge, wax, and perhaps glass,
which plow out shallow channels in the surface. Beeswax-coated tools are
particularly bothersome in this respect. One method of avoiding sleeks
is to allow the tool to run nearly dry before each application of fresh
rouge. The optician calls this "drying up each wet." This probably causes
the surface of the tool to become quite warm, allowing the pitch surface
to flow rather rapidly and to renew itself.
Large lenses and
very soft materials are best polished by coating the surface of the polisher
at regular periods with fresh pitch or beeswax. The polishing tool is
to be coated at intervals of 1 to 3 hours. The beeswax is applied to the
facets of the tool with a swab made of cheesecloth bound on a short stick.
It is advisable to have the wax smoking hot and to apply as thin a coating
as possible. In polishing speculum metal, which scratches rather easily,
the fresh beeswax coating is to be charged with dry rouge. The rouge is
applied to the facets with the tip of the finger.When a full polish is
achieved, that is, when the grinding pits are entirely removed, the work
is ready for testing and figuring. A convenient and simple test for full
polish is to focus sunlight on the glass surface with a lens. The focus
of this lens does not heat the glass much, but light scattered by pits
in the surface is quite conspicuous if the surface is not fully polished.
To avoid introducing
astigmatism into the work during polishing, it is frequently rotated a
fraction of a revolution with respect to the supporting table in order
to distribute the effect of edge arcs symmetrically around its periphery.
Figuring.
Figuring is the process whereby a polished surface has its shape altered
by local working with polishing tools. For example, a spherical surface
is made aspheric, or undesirable zones or astigmatism is removed.
Sometimes in figuring
plane parallels or prisms the effect of inhomogeneities in physical properties
of the glass can be corrected (in first approximation) by slight deviations
from flatness in the surfaces.
The general procedure
in figuring is one of trial and error. Testing is alternated with local
polishing on those areas which are high in reference to a desired surface.

Fig.
17. Cutting zones for various tools. |
Cutting zones
and transition zones. The behavior of the polishing tool depends on
its size, character of facetting, shape, and the manner in which it is
manipulated on the work. There is no way in which a tool may be manipulated
so that it will remove glass from a surface uniformly. Rather, each manipulation,
if carried out on a perfectly flat surface, tends to produce its own characteristic
zones, which will be referred to as the cutting zones of the tool. Figs.
17 and 18 illustrate the cutting zones of some typical tools. These zones
are defects in the mirror surface symmetrically positioned about the center
of the work. The figuring procedure consists in testing the imperfect
surface and working it with a suitable tool whose cutting zones will tend
to cancel the zones revealed by the test.
Sharp zones are first
"softened" with a large tool coated with soft pitch. This procedure applies
both to those zones remaining from polishing and to those which may appear
during the figuring. The latter are usually transition zones resulting
from imperfect cancellation of a smooth zone in the work by the cutting
zone of the tool. This is illustrated by Fig. 20. After the sharp zones
are softened with a soft pitch tool, the optician tests again to determine
the figure. To carry the figuring farther, a satisfactory surface tangent
to the "valleys" of the surface, lying wholly within the glass, is imagined,
and the hills relative to this imagined surface are polished away with
an appropriate tool and stroke. This cycle of testing, polishing in a
manner such that the cutting zones improve the figure, testing, smoothing
transition zones with a soft tool, testing, and so forth, is continued,
until the necessary figure is attained.
Interpretation
of the action of polishing and figuring tools. If we could assign
quantitative values to all of the factors influencing the cutting action
of any given tool and stroke, we could conceivably predict the cutting
zone for it. However, we cannot do this; but we can describe the factors
qualitatively as they are appraised in the minds of opticians.
First, the polishing
tool cuts away the glass in proportion to the time the tool is passing
over the glass.
Second, the tool
cuts faster as the speed increases. The cutting or polishing rate is not,
however, proportional to the speed at which the tool passes over the work.
Third, sections of
the tool which overhang the work during a part of the stroke cut relatively
faster than the sections which do not overhang the work.
Fourth, the facets
of the tool which lead cut faster than following facets, because new rouge
available to the leading facets is wiped away from the path of following
facets.
Fifth, the tool cuts
fastest where the pressure on it is greatest, everything else being equal.
This accounts for the selective action of the full-size tool on high zones,
which action is the basis of all figuring. It is important to give this
factor careful consideration in working aspheric surfaces, in which the
tool naturally works in a way that tends to Ib return the surface to a
sphere.

Fig. 18. Cutting
zones for various tools. |
Figuring tools
for zones. Figs. 17 and 18 show various-shaped tools and illustrate
the zones which they would b ordinarily produce in a true flat surface
when worked with both long and short strokes. The stroke in each case
is a thin oval across the center of the work. The use of an oval stroke
has an advantage over a straight reciprocating stroke ilt in that the
tool never comes to a complete stop.
It will be noted
from Fig. 17 that the full-size tool makes the work more convex by an
amount which increases with the length of the stroke. Intermediate-sized
tools, as the 6 size, hardly change the over-all curvature of the work
when a long stroke is used, while a short stroke with this tool 3 makes
the work more concave. Smaller tools make the work more concave.
It will be further
noted that the effect of the tool in changing the over-all curvature is
(except for the case noted) greater than its effect in producing cutting
zones. This change of curvature is generally inconsequential, except where
one is making flats or striving for a radius of curvature specified to
extreme precision.
Fig. 18 shows the
action of ring and star polishing tools.
The behavior of tools
on short radius curves may differ considerably from their behavior on
flats. Figs. 17 and 18 refer to flats.
As testing methods
are not very precise and the polishing methods even less so, it is well
to approach the desired surface carefully and slowly, with periods of
polishing interrupted frequently for testing. This allows one continually
to change the "stratagem according to the tactical situation and nature
of the terrain."

Fig.
19. |
One should use a
clock to time the work done with a given polishing tool. If a mirror is
improved by a certain treatment of 20 minutes' duration and the test shows
that about as much more work is required, it is advisable to continue
the treatment for 10 or 15 minutes more and test again in order not to
overreach the desired result. It must also be emphasized that tools may
cut faster at first than later, so that the significance of the time factor
should not be taken too seriously. Also, the behavior of any given tool
may be erratic. It is best to try it for short periods at a time with
frequent testing in order to be certain of its action. Inasmuch as the
figuring procedure should not be hurried, beeswax-coated tools, which
polish about three times as fast as uncoated tools, are not used for figuring.
During the final stages of figuring, when delicate testing is required,
the work should be allowed to stand on the testing support for sufficient
time to allow complete equalization of temperatures.

Fig. 20. |
Pressing the tool
through coarse cloth (such as an onion sack) gives many small facets in
addition to the large facets. This results in quick contact of the tool
to the glass and smooth action of the figuring tool from the start. (See
Fig. 19.)
To avoid astigmatism,
the work should be occasionally rotated on the supporting table. In addition,
with small tools it is important always to work the tool around the optical
surface through an integral number of revolutions.
Hard tools tend to
maintain a surface spherical or flat and are useful for generating fiats
or mirrors which are being worked to a specified radius. On the other
hand, soft tools are recommended for working aspheric surfaces. Mirrors
made by amateurs may exhibit a better figure than mirrors turned out by
professional workers: The reason for this lies in the fact that amateurs
usually use soft tools, which produce smooth flowing zones. On the other
hand, professional opticians have the skill and knowledge to remove zones
quickly with harder tools. In many cases, this rapid working produces
faint transition zones, which show up under the most severe testing conditions.
It is characteristic of the commercial optician that he will produce a
figure as good as, but no better than, that which his specifications call
for.

Fig.
21. |
Manner of figuring
various zonal defects, and of making aspheric surfaces of revolution.
Focograms and exaggerated profile curves illustrating the manner of figuring
various symmetrical defects are shown in Figs. 20, 21, 22, and 23. The
interpretation of focograms is described in a later paragraph. At the
upper left of Fig. 20 we see the focogram and exaggerated profile of a
mirror with turned-down edge. This is corrected as follows: A 5/6-size
tool and short stroke is used. Two cutting zones are produced. One zone
is positioned where the leading edge of the tool comes to the extreme
limit of the stroke, and the other is positioned where the trailing edge
of the tool comes to the limit of the stroke. Besides making cutting zones,
the tool has the further effect of making the figure more concave. The
result is to change the full-line profile curve at the top left of the
figure or the dotted profile curve at the top center to the profile exhibiting
two sharp transition zones, as shown by the full curve at the top center
and right. These transition zones are then smoothed off with a full-size
soft tool with relieved edges (to avoid a turned-down edge), using a short
stroke.
The treatment with
a 5/6-size tool, as described above, is suitable for removing a turned-down
edge from a circular flat; since the final treatment with a soft tool
makes the work more convex (see Fig. 17), one can, by the judicious balance
of the work done with the two tools, balance the increase in concavity
produced by the first by the increase in convexity produced by the second.
Fig. 20 shows the procedure applied to a spherical surface.

Fig. 22.
|
The sketches at the
top of Fig. 21 show how a turned-up edge is turned down with a full-size
soft tool.
The second series
of sketches of Fig. 21 shows two methods of figuring to remove an intermediary
depressed zone. The profile of the full line at the left or the dotted
line in the center is changed by the indicated treatment, shown in the
center, to the full-line profile in the center or the dotted-line profile
at the right. In turn, this is changed by the indicated treatment to the
spherical curve represented by the full-line profile at the right. In
the first treatment the existing dotted profile, center, is elevated at
the center and has a turned-up edge in reference to the imagined curve
represented by the full-line profile. This imagined curve is realized
with a sub-diameter tool. At the right the full line represents the imagined
surface which is realized by removing the narrow sharp transition zones
with a full-size soft tool. Inasmuch as this treatment does not change
the radius of the work, it is suitable for figuring flats.

Fig.
23. |
By the alternate
treatment, which decreases the concavity of the mirror, the cutting zones
of the soft full-size tool change the intermediary depressed zone (depressed
in reference to an imagined spherical surface) to two sharp elevated zones
on a second imagined spherical surface. These elevated zones are then
managed with a sub-diameter soft tool as illustrated.
Two treatments for
a small depressed zone near the center of the work are illustrated in
the bottom series of Fig. 21. By one, the first imagined surface lying
wholly under the glass surface requires the removal of an outer layer
represented by the difference between the dotted starting profile in the
center and the full-line final profile in the center. The next imagined
surface, now a spheric one, leaves several sharp zones to be removed by
the usual treatment with a full-size soft tool.
The alternate treatment
goes from the primary defective surface to one with an intermediary elevated
zone relative to the desired spheric surface. A chordal stroke is used.
The elevated zone is removed by a second larger-size tool.
In working on small
zones in large mirrors or relatively large zones in small mirrors the
optician has as possible figuring tools the thumb, the fingers, and the
ball and heel of his hand.
Fig. 22 shows how
a narrow elevated zone may be removed with the thumb and how a depression
may be removed with tools from which a facet has been removed. The thumb
is used with extreme caution, applied lightly for one revolution at first,
and then, if necessary, for a few more complete revolutions. There is
a danger of overcompensating for the elevated zone with the cutting zone
of the thumb, because small polishing tools cut very rapidly.
In testing an optical
surface which has been figured by the fingers, one must allow enough time
for the heat developed by the friction of the fingers to be dissipated.
Even for one revolution, this heating will produce a false zone, by expansion
of the glass, which may be higher than the original zone.
The top of Fig. 23
shows how a spheric mirror can be parabolized with a star tool. The focogram
at the top right gives the appearance of the parabolic surface when it
is tested at the center of curvature. The focogram of a parabolic profile
tested at the mean center of curvature exhibits the character of a soft
raised intermediary zone.
The second series
of Fig. 23 shows an alternate parabolizing procedure and focograms of
the appearance of the figure of the mirror, as tested at the focus, before
and after the use of the method. The advantage of testing a parabolic
mirror at the focus is evident: Thc optician works toward a uniform distribution
of light over the mirror face. The advantage of testing at the focus over
testing at the center of curvature is especially great when zones are
being removed. Zones which are practically invisible if the mirror is
examined at the center of curvature become quite conspicuous when it is
tested at the focus.
The last two series
of Fig. 23 show procedures that may be used for hyperbolizing.
Astigmatism.
The correction of astigmatism is more difficult than the removal of central
symmetric zones. Cylindrical defects and, in general, all defects which
are not symmetrical about the center of the work produce astigmatism.
These defects must be worked out by hand. The rule of procedure is the
same as it is for zonal defects–namely, the polishing is done on
the high portions of the surface Transition zones are removed with a full-size
tool in the regular manner. The simplicity of this rule must not, however,
be allowed to obscure the fact that the correction of astigmatism is one
of the most delicate operations required of the optician, and that aside
from a knowledge of what is to be done it requires considerable manual
dexterity. The tendency of tools to cut fastest near their periphery and
especially where their edges come to rest is to be continually kept in
mind. The complete removal of astigmatism ir. an optical surface is the
apogee of good workmanship, while its avoidance is the result of experience.
Optical testing.
There are many applications for optical tests besides their employment
to gLude figuring. For example, one may wish to know the figure of a finished
spherical concave mirror, a flat, or perhaps a lens of unknown quality.
Also, the testing methods described here can be used to test gratings.
The Foucault knife-edge test is employed by the Schlieren-methods for
photography of sound wave fronts.6
Newton's fringes.
The simplest optical tests are interference tests using monochromatic
light of wave length 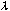 . The
fringes manifest by a thin air film between optical surfaces are called
Newton's fringes. They represent lines of equal optical separation of
the surfaces. Between two adjacent fringes the optical thickness of the
air film varies by an amount . The
fringes manifest by a thin air film between optical surfaces are called
Newton's fringes. They represent lines of equal optical separation of
the surfaces. Between two adjacent fringes the optical thickness of the
air film varies by an amount 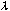 /2,
and the fringes may be interpreted as contour lines for the surface of
one glass referred to the surface of the other glass, which is usually
a flat or spherical test surface. /2,
and the fringes may be interpreted as contour lines for the surface of
one glass referred to the surface of the other glass, which is usually
a flat or spherical test surface.
The fringe system
between two flats, if they are slightly inclined to each other and are
illuminated with monochromatic light, is a series of parallel equispaced
straight lines.

Fig. 24. |
A cylindric surface
of long radius of curvature in contact on a line with a flat gives straight
fringes of unequal spacing.
A spherical convex
or concave on a flat gives concentric circles.
Fig. 24 illustrates
a box for testing optical surfaces in contact with a flat and the appearanee
of the fringes under different eonditions.
The appearanee of
a convex spheric or cylindric surface on a flat is the same as the appearance
of a concave surface. The difference in distance between the surfaces
at one fringe and at the adjacent fringe is 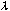 /2;
but the sign of the difference, that is, whether the separation is increasing
or decreasing, is not known. The following rule may be employed to differentiate
between a concave and a convex surface. The exhibited curved fringes expand
away from their center of curvature when the head is lowered or moved
away from the normal to the flat if the surface is convex, while, if it
is concave, they contract toward their center of curvature. /2;
but the sign of the difference, that is, whether the separation is increasing
or decreasing, is not known. The following rule may be employed to differentiate
between a concave and a convex surface. The exhibited curved fringes expand
away from their center of curvature when the head is lowered or moved
away from the normal to the flat if the surface is convex, while, if it
is concave, they contract toward their center of curvature.
Newton's fringes
are particularly suited to making a comparison between a "flat" of unknown
quality and a master flat. Also, they may be employed for testing surfaces
of a definite radius by pressing them against a master plate of the same
radius but opposite curvature. In this case, white light rather than monochromatic
light is generally used, and deviations from the master are determined
by the residual color of the interference pattern.

Fig.
25. |
When precision tests
are made of a "flat" against a master flat and the fringes are observed
at other than normal incidence, it is necessary to have the fringes running
parallel to the plane of reflection, or they will be curved, even though
the work is flat. Deviations of the fringes from a straight line are estimated
by comparison with a stretched wire or thread.
Haidinger's fringes.
Haidinger's fringes are excellent for testing the quality of plane parallels.
Fig. 25 shows how Haidinger's fringes are observed. The usual manner of
observing Haidinger's fringes is shown at the right in Fig. 25, and the
appearance of the fringes and their positioning in respect to the reflected
image of the observer's eye are shown in the lower right of this figure.
These fringes are arranged like the Newton's fringes produced by a sphere
on a plane They are different in that Newton's fringes are observed by
focusing the eye on the thin air film between the plane and sphere, whereas
Haidinger's fringes are observed at infinity either with the eye or with
a telescope. Newton's fringes represent the locus of points of equal optical
thickness, while Haidinger's fringes represent the locus of points where
rays "from the eye" make equal inclination to the planeparallel plate.
The Haidinger fringes are observed at normal incidence, and the plane-parallel
plate is moved laterally to apply the test to different areas of the work.
A variation of thickness, from one end of a plane parallel to the other,
results in the appearance or disappearance of fringes. If the plate gets
thicker, fringes appear. The appearance and disappearance of one ring
corresponds to 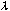 /2n change
in thickness. For the most delicate testing, a telescope is used. A large
field telescope equipped with a filar micrometer may be used to measure
the diameter of the rings. With this telescope the appearance of about
one tenth of a ring can be detected. For glass having an index of 1.5,
one tenth of a ring represents a difference of thickness of 1.5 X 10 /2n change
in thickness. For the most delicate testing, a telescope is used. A large
field telescope equipped with a filar micrometer may be used to measure
the diameter of the rings. With this telescope the appearance of about
one tenth of a ring can be detected. For glass having an index of 1.5,
one tenth of a ring represents a difference of thickness of 1.5 X 10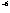 cm or approximately 0.5 X 10-
cm or approximately 0.5 X 10-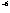 inch.
inch.

Fig. 26. Eyepiece
image test. |
Eyepiece tests.
Another important means of examining the quality of image-forming systems
of mirrors or lenses is to inspect an imaged pinhole light source. A high-power
magnifier, such as a 14X Hastings triplet, is suitable for examining the
image. This test is called the eyepiece test because it is essentially
the test which is applied when one observes a star in the eyepiece of
an astronomical telescope on a good night. The eyepiece test is the most
sensitive optical test for astigmatism. The infrafocal and extrafocal
images should be examined, as well as the focal image. It is advisable
to record the results of this test by drawing rough distribution curves
representing the light intensity along a horizontal diameter of the image.
Fig. 26(a) illustrates eyepiece images for a good (though not perfect)
spheric mirror tested at the center of curvature. Fig. 26(b) illustrates
the eyepiece test for an overcorrected parabolic mirror tested at the
center of curvature' and (c) illustrates the test applied to a mirror
with very slight astigmatism.
Fig. 33 illustrates
the eyepiece test in comparison with the Foucault, Ronchi, and Hartmann
tests.

Fig.
27. |
Foucault knife-edge
test. The Foucault knife-edge test is 16 usually employed for the
detection of central spherical aberration, particularly in testing work
of fairly large aperture, such as lenses or mirrors used for astronomical
telescopes.
The test is simplest
as applied to a spherical concave surface of long radius. A small hole
is pierced in thin metal sheet with a sharp needle and illuminated by
means of a lamp, together with a suitable optical system.7
This hole is located near the center of curvature of the mirror. (See
Fig. 27.) Light from it is reflected by the mirror to form an image at
an equal distance on the opposite side of the center of curvature. When
the eye is placed behind this image so as to receive light from all parts
of the mirror, the whole aperture will appear evenly illuminated. Then
if an opaque screen, the so-called knife edge, is moved laterally across
the focal point, the whole aperture will appear to darken evenly, that
is, if the mirror is truly spherical, as in Fig. 27(ii) If the knife edge
is moved across the cone of light a short distance inside the focus, its
shadow, as it appears on the mirror, moves in the same direction as the
knife edge, Fig. 27(i); if it is placed outside the focus, the shadow
moves in the opposite direction, Fig. 27(iii). It is possible by this
means to locate the focus of the mirror with great precision.

Fig. 28. Arrangement
for carrying out the Foucault test: (a)
Testing of a spherical mirror at the center of curvature. (b)
Testing of a short-focus spherical mirror. (c) Testing a flat
with an auxiliary spherical mirror. If knife-edge and pinhole
move together, a lack of flatness represented by a sagittal distance
h introduces astigmatism between horizontal and vertical
focus. The relationship between h and 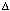 R
is given. (d) Zonal testing of a parabolic mirror at the center
of curvature. R is the radius of the curvature at the center.
(e) Testing of a parabolic mirror at the focus with starlight.
(f) Testing of a parabolic mirror at the focus with an auxiliary
testing flat. (g) Alternate procedure for testing a parabolic
mirror with a flat. (h) Testing of a hyperbolic mirror with a
special testing mirror. (i) Testing of a hyperbolic mirror with
a parabolic mirror and flat. (j) Testing og an elliptic mirror.
(k) and (l) Testing of a Schmidt lens. R
is given. (d) Zonal testing of a parabolic mirror at the center
of curvature. R is the radius of the curvature at the center.
(e) Testing of a parabolic mirror at the focus with starlight.
(f) Testing of a parabolic mirror at the focus with an auxiliary
testing flat. (g) Alternate procedure for testing a parabolic
mirror with a flat. (h) Testing of a hyperbolic mirror with a
special testing mirror. (i) Testing of a hyperbolic mirror with
a parabolic mirror and flat. (j) Testing og an elliptic mirror.
(k) and (l) Testing of a Schmidt lens.
|
In the case of an
imperfect mirror, such as the one shown in Fig. 27(iv), all rays do not
converge to a single point, and if the knife edge intercepts the converging
light rays as reflected from the mirror, the aperture will appear to be
unequally illuminated; some rays are completely cut off by the knife edge,
whereas others pass by it and so reach the eye. The mirror shown at the
right has an intermediary raised zone. For the inside half of the zone
(c) the focal length is shorter than it is for the outside half (b). With
the knife edge advanced into the mean focus of the converging rays, those
rays from the areas which have their center of curvature exactly at the
position of the knife edge are attenuated; rays from (c) reach the eye
without attenuation, while rays from (b) are cut off entirely by the knife
edge. Accordingly, (c) and (b) appear very bright and dark respectively.
The appearance of
the mirror with the knife edge and eye in the positions indicated is as
if it were made of plaster and illuminated at grazing incidence with an
imaginary light source.8 Usually the pinhole source is on the
right side of the center of curvature and the eye on the left. In this
case, if the knife edge cuts the image from left to right, the observer,
thinking of this imaginary light source as illuminating the plaster disk
from the right, interprets its shadows in accordance with their apparent
inclination. For a lens, the observer interprets the shadows by thinking
of the illumination as coming from the left.
Various more complicated
setups for making the Foucault test are shown in Figs. 28 and 29. In these
two figures a test mirror or lens of unquestioned quality (or at least
of known quality) is shown clear, while the tested mirror or lens is cross-hatched.
Zonal knife-edge
testing. Aspherical mirrors, such as paraboloidal ones, can be tested
at their mean center of curvature without an auxiliary testing flat by
measuring the radii of curvature of the glass at various zones. The mirror
is covered with a diaphragm of cardboard with holes opposite the zones
to be tested. The simplest diaphragm has holes at the center, at the edge,
and at 0.707 of the radius, as illustrated in Fig. 30. If the mirror is
parabolic, the characteristic shadow shown in the upper right of Fig.
23 will appear when the mirror is viewed without the diaphragm. With the
diaphragm, the measured difference in focus of the center and the zone
at the rim will be r2/2R, where R is the mean
radius of curvature of the mirror and r the radius of the mirror. This
test is suitable for testing small mirrors to determine when a raised
intermediary zone, as illustrated in Fig. 23, is carried sufficiently
far to parabolize the mirror.

Fig.
29. Foucault tests for achromats to be used to focus parallel light
and diverging light. Also, tests for a microscope objective and
a prism. |
Diaphragms for very
large parabolic mirrors, or mirrors of focal ratio of f/4.5 or
greater, are constructed so that the radius of curvature of a large number
of zones can be measured. Ordinarily, mirrors of aperture f/10
or less need not be parabolized unless their diameter is greater than
24 inches.
Another procedure
for quantitative application of the knife-edge setup has been described
by E. Gaviola.9 By this procedure the inclination of different
zones is determined relative to a mean surface for the mirror by measuring
the position of the knife edge which intersects the light rays reflected-from
these zones.

Fig. 30. |
In any knife-edge
setup, and especially where accurate quantitative zonal measurements are
to be made, it is important to avoid parallax. Although a setup like the
one shown in Fig. 27, using a simple pinhole and knife, is suitable for
qualitative tests on small mirrors of long radius, a more elaborate setup
is usually required.
Parallax appears
whenever a Foucault test is made on more than one mirror, such as a test
on a parabolic mirror at its focus with an auxiliary flat. (See Fig. 28.)
This parallax is due to the fact that a ray from the pinhole strikes the
parabolic mirror at one point and is subsequently reflected, after returning
from the flat, at a different point on the parabolic mirror. The displacement
between these points on the paraboloid mirror is somewhat less than the
displacement between the pinhole and the knife edge. Even so, the displacement
may be sufficient to yield results that are quite misleading. As a result
of parallax one does not get an indication of the character of the mirror
at either of the two indicated points but rather a kind of average for
the two points. This information is of little value and may 1' be quite
misleading if the effect of errors at one point of the parabolic mirror
is compensated by opposite errors at the other.

Fig.
31. |
A knife-edge testing
device is illustrated in Fig. 31. Fig. 32 shows two attachments for it
which may be used to avoid parallax. The device at the left eliminates
parallax by eliminating the displacement between the knife edge and the
pinhole a virtual image of the pinhole formed by means of a half-silvered
pellicle mirror lies exactly on the knife edge. A pellicle mirror is made
by flowing lacquer on an inclined glass plate. After the lacquer is hard,
it is stripped off the glass under water. The film of lacquer is then
mounted on the flat surface of a brass frame and half- silvered by the
evaporation process.
The device at the
right uses a slit instead of a pinhole. This device avoids parallax by
the simple expedient of removing it by half a revolution in azimuth from
the testing diameter.

Fig. 32. |
The Ronchi test.
The Ronchi test will be treated here only briefly, since it is not
widely employed and its interpretation is not simple.10 A small
light source illuminates the mirror through a ruled surface (about 100
lines per inch), and the image is also formed through another section
of the same ruled surface. For comparison, the Foucault test of a defective
mirror is shown at the top of Fig. 33. Below, we have the results of the
eyepiece test and Ronchi test of the same mirror, and, at the bottom,
the Hartmann test is illustrated. Fig. 34 shows a simple quick way of
testing a lens with the Ronchi screen. A good lens gives straight Ronchi
lines.

Fig.
33. Comparison of Foucault, eyepiece, Ronchi, and Hartmann tests
of a defective mirror. |
Hartmann's test.
Hartmann's test is similar to the Ronchi test for a lens, illustrated
in Fig. 34. A diaphragm, such as the one shown at the bottom left of Fig.
33, is prepared with several appropriately spaced holes. This diaphragm
is placed directly in front of the mirror or lens. The Foucault test determines
errors in the mirror by the lateral positioning, relative to their neighbors,
of various rays as they pass through the focus; the Hartmann test determines
the positions of these rays, relative to their neighbors, at points either
inside the focus at (e) or outside of the focus at (f). The relative position
of the holes in the plate and the appearance of the rays, as observed
with the eyepiece at (e) and (f), are shown in the figure.11
The advantages of
the Hartmann test over the others illustrated in Fig. 33 are that it is
not necessary to locate the mean focus, and that the results of the test
are easily recorded photographically, both of which features make it particularly
useful for figuring lenses for the ultraviolet region of the spectrum.
Lining up a system
of mirrors. In the more complicated testing setups shown in Figs.
28 and 29 it is often quite difficult to get the mirrors or lenses lined
up. The appearance of coma in the eyepiece image, however, can be used
to advantage for this. The coma of a system not properly lined up is quite
strong and indicates clearly in what direction the mirrors are to be adjusted
to get round images.

Fig. 34. |
Some opticians put
two white threads at right angles to each other across the face of one
of the mirrors. When these threads and all of the secondary images af
them viewed from the focus appear symmetrical, the system is in alignment.
Two methods of
generating optical surfaces. As we have already pointed out, the optician's
task is defined as the generation of accurate surfaces on mirrors, lenses,
prisms, and so forth, which possess a high polish. This is ordinarily
done by hand or with the modified Draper machine, as described before.
Or it may be done with a high-speed hand-lever machine in the manner described
below. The procedure with a modified Draper machine or by hand is slow,
but it yields the most accurate results. The modified Draper machine illustrated
in Fig. 10 uses a single crank and allows for counterbalancing of the
tool, automatic control of the tool, slow smooth stroking, and easy placement
of the work. In contrast with this, the hand-lever machine shown in Fig.
35 features high speed and simplicity. The spindle is run at about 100
to 600 r.p.m. Naturally, the heat thus generated, as well as the high
speeds of cutting, makes work of the highest precision impossible.

Fig.
35. |
Working optical surfaces
on the hand-lever machine. The tool used with the hand-lever machine may
be attached to a high-speed spindle as shown in Fig. 35, or the work may
be attached with wax to the spindle and the tool applied above. In the
former case, a socket for the pivot point of the hand lever is waxed to
the work with a mixture of 2 parts coal-tar pitch to 1 part sieved wood
ashes. When the tool is applied above, the socket is turned in the back
of it.
The preliminary grinding
may be accomplished on the I hand-lever machine with a sub-diameter ring
tool of iron, as with the Draper machine. When this ring tool is moved
back and forth across the center of the spinning work with a short stroke
so that there is no overhang of the tool, the surface is made concave.
A long stroke with overhang gives a convex surface. The tool is pivoted
and allowed to spin freely, and 90 Carborundum with water is fed on it
to accomplish the grinding. The growth of the curve in the work is measured
with templates. These are usually cut on a lathe from a thin sheet of
brass or bronze.

Fig. 36. |
The final grinding
is done on the hand-lever machine with a spherical brass tool of the same
diameter as the work. The spherical tool is made as follows: A brass male
and female part are turned on the lathe to the same curvature in the manner
illustrated by Fig. 36. These are then lapped together with Carborundum
to generate complementary spherical surfaces. If a lathe is not available,
they may be separately ground with the hand-lever machine to an approximate
fit with a third metal ring tool and then lapped together. It is important
to cut a cavity in the center of the one to be used as the grinding tool.
The cavity should have a diameter of about one twentieth of the tool diameter.
After the proper
curve is approached in the work by grinding with the ring tool, the spherical
brass tool is substituted, and the final grinding is carried out with
90, F, and 600 Carborundum and 302-1/2 emery. During the grinding process
the offset of the tool in respect to the work should never be so great
that the tool and the work rotate in opposite directions.
Polishing is accomplished
on the hand-lever machine with rouge on a pitch lap. The brass tool used
for grinding may be warmed and coated with a layer of hard pitch or pure
beeswax for polishing. While the wax is still warm, it is pressed to the
proper shape with the already fine-ground work (wet with soap and glycerin
solution) to give a layer of pitch about 1/8 to 1/4 inch in thickness.
As for grinding, this lap is cut away in the center to form a cavity of
one twentieth of the tool diameter. Also, the pitch is cut to form annular
grooves. These grooves facilitate contact between the pitch and the work.
The pitch lap should be frequently trimmed.
If the central cavity
removed is too broad, the tendency is to polish the edges first, while
if the central cavity is small and pitch is trimmed off the edges of the
tool, it will polish the center first. Also, whether the polish progresses
faster in the center of the work or near the edge depends on the offset.
A little offset favors polishing the edges fast, and a big offset makes
the progress of polishing greater in the center. One can easily keep track
of the progress of the polishing by shining a strong light on the work
and observing the "grayness" produced by the residual grinding pits.
It is difficult to
balance all these factors, and in practice one should observe how the
polish progresses. If the polish is not progressing satisfactorily, the
offset can be altered or the tool trimmed accordingly.
Figuring aspheric
lenses on the hand-lever machine is accomplished by polishing with sub-diameter
tools and star or ring tools.
Small lenses are
aligned on the spindle by tilting them while the blocking wax used to
cement them in place is still warm. The spindle is turned slowly, and
if an object, preferably a small light source, seen reflected in the surfaces
does not describe an eccentric circle as the lens rotates, the alignment
is complete.
After being centered
on a brass tube mounted in the head-stock of the lathe, in the same manner
as described above, the work is edged with an iron tool and grits. (See
Fig. 6.)
Relationship between
two optical surfaces. Although we have emphasized the phases of procedure
which are important in generating the optical surface, we have not dealt
extensively with the orientation of that surface with respect to the general
form of the work or with respect to other optical surfaces. These are
matters usually managed in an obvious manner. However, in the construction
of prisms, especially right-angle prisms and plane parallels, the manner
of getting proper relationship between the two flat surfaces involved
is not so obvious. A half-hour of polishing on the Draper machine or a
few minutes of polish. During on the spindle machine will usually put
enough polish on ground surfaces to allow their relationship to be tested
on a spectrometer table or with other optical tests. Right-angle prisms
are tested by employing their property of deviating a light beam exactly
180 . This test is sensitive
to about 1 minute of angle when it is made with the naked eye, and if
it is made using a telescope equipped with a Gauss eyepiece, it is sensitive
to about 1 second of angle. . This test is sensitive
to about 1 minute of angle when it is made with the naked eye, and if
it is made using a telescope equipped with a Gauss eyepiece, it is sensitive
to about 1 second of angle.

Fig.
37. |
Plane parallels are
ground to be flat and parallel to about 1/20,000 of an inch. Good micrometers
are used to test the glass for parallelism to this accuracy. The final
optical precision is obtained by figuring. The test using Haidinger's
fringes, described before, is used to guide the figuring. Plane parallels
are usually made with circular faces to be cut up later into rectangles
if necessary.
Blocking.
Inasmuch as round glass surfaces are more easily figured than square or
rectangular ones, it is advisable to mount a prism blank in a metal ring
as shown in Fig. 37, together with auxiliary glasses having the same coefficient
of expansion, to make up a circular array of glass surfaces. This circular
array is held in the metal ring with plaster of Paris, and the ensemble
is then worked as a single disk of glass. The parts may be immersed in
a single thick layer of plaster, but it is best to imbed them in a double
layer of plaster as shown in Fig. 37. A mixture of 3 parts plaster to
2 parts water is used. This gives an almost nonshrinking, although not
very strong, cement. The work may be coated first with a thin layer of
beeswax in cases where free lime or moisture in the plaster might attack
the glass. After the plaster of Paris sets, its surface is shellacked
to make it impervious to water. The grinding and figuring should be finished
in one day. Otherwise, owing to "aging" of the plaster, the central and
auxiliary surfaces will not maintain satisfactory alignment.

Fig. 38. |
Quartz and calcite.
When optical surfaces are generated on crystals, it is frequently required
to orient the surfaces precisely with respect to the crystal axes. Fig.
38 illustrates the manner in which the optical axis of quartz is precisely
located. The crystal is cut at each end with the mud or diamond saw, the
cuts being made roughly perpendicular to the optical axis. These parallel
saw cuts are then ground with the abrasives to grade 150 Carborundum and
"artificially polished" by cementing cover glasses to the ground ends
with balsam. Polarized light is used to determine the optical axis in
the manner illustrated in the figure. The system of rings noted through
the analyzer will remain stationary when the crystal is rotated about
a vertical axis if the cuts are perpendicular to the optical axis. If
the rings "wobble" as the crystal is rotated, the axis of rotation is
to be tilted by means of the gimbals provided (or with wedges) until the
fringes are stationary during rotation. The ends are then recut, taking
account of refraction (see note on the figure), and the plate retested
to check the result.
When properly cut
quartz crystal is rotated in a clockwise direction, the rings close in
toward the center if the crystal is left-handed quartz and move out if
it is right-handed quartz.

Fig.
39. Calcite: (a) Orientation of axis. (b) Cuts for making Nicols.
(c) and (d) Procedure for cutting calcite to make Nichols. |
An irregular piece
of quartz can be roughly examined for striae by immersion in a tank filled
with a solution composed e of 80 per cent ethyl cinnamate and 20 per cent
xylol (by volume). Iron oxide surface stains may be removed from the crystal
by washing in oxalic acid solution.
The orientation of
the principal axis of calcite is shown at the top of Fig. 39. To cut calcite
for making Nicols, the crystal is oriented and mounted in a wooden form
having the cutting plane defined by a preliminary saw cut. The cut through
the crystal is made by hand by sawing through both plaster and crystal
with a hard-drawn copper wire mounted in a scroll-saw frame and charged
with Carborundum.
Optical working
of crystals. Quartz is the optician's favorite medium. Both the fused
and the crystal material are ground and polished by the same procedure
as glass.
Calcite crystals,
especially large ones, are expensive, and e in addition they are soft
and easily fractured. Accordingly calcite is always worked by hand with
very light pressures. All but the smaller Carborundum grains tend to produce
fractures in calcite, and therefore the series F-400-600 Carborundum and
302-1/2 and 303-1/2 emery is recommended for working it. If prisms with
very thin edges are to be made, 400 Carborundum is used as the coarsest
grit. A beeswax coated pitch lap is satisfactory for polishing and figuring
calcite. For figuring, calcite should be blocked with calcite of the same
crystal orientation.

Fig. 40. |
Rock salt is polished
and figured on a hard-pitch tool pressed with a glass pressing lap.12
The desired figure is obtained with an overcorrected pressing lap, as
the figure obtained on this material is usually convex with respect to
that established in the tool by the pressing lap. For example, in making
flats, one would use a slightly concave pressing lap (1/1000 of an inch
in a 4-inch disk or 60-foot radius of curvature). Rouge in saturated salt
solution is used to start the polishing. Fig. 40 shows the arrangement
of the pitch tool which is placed below the work, and a chamois skin used
for drying the work. The work is rubbed against the lap until the rouge
is almost dry. It is then kept moist with the breath for the final strokes
and is slipped off the tool onto the chamois to be dried. This technique
should be practiced on test pieces before big work is undertaken. The
first face of a prism or lens is lacquered or waxed to prevent attacks
by moisture while the second face is being worked. The pitch tool is coated
with beeswax. Beeswax is useful for even softer materials than rock salt,
such as potassium chloride, potassium bromide, and even potassium iodide.
Polishing of metals.
Perhaps the most important metal in optics is speculum metal. It is very
hard, exhibits a conchoidal fracture like glass, and is worked by the
same procedure, being ground with the same sequence of grits. The polishing
tool should have narrow facets. It is often advantageous to do the final
figuring of speculum surfaces with the metal face turned down to avoid
scratching.
Stellite is also
worked like glass except that longer grinding periods (two to three times
that for glass) are required. Ordinarily pitch polishing tools are used
with rouge or chromium oxide as polishing agent. One should try to "hold"
the figure from the grinding stages until polishing is completed.
Hard steel is worked
in the same manner as glass.
In grinding soft
steel, a still softer metal, such as copper or lead, is used as a grinding
tool.
Soft steel and hard-drawn
copper are difficult to polish, but they can often be managed with a polishing
tool coated with a mixture of paraffin and oxide of tin. As much oxide
is added to the molten paraffin as it will take without crumbling. This
mixture is applied hot with a swab to the pitch polishing lap.
If a metal tends
to etch or discolor during polishing, it is advisable to try carbon as
a polishing agent (charcoal ground in a ball mill and washed). Chromium
oxide will often give a bright polish in cases where rouge would discolor
the metal.
The very soft metals–silver,
soft copper, gold, and so forth–cannot be easily surfaced by the
ordinary optical methods. They become charged with the grits and refuse
to grind. Silver circles are brightened by rubbing moistened cigarette
ashes with the thumb back and forth in a direction parallel to the engraved
lines.
The Schmidt camera.
The Schmidt camera is an image-forming device which combines features
not possessed by any lens system, and, while it has some disadvantages,
it may well prove to be a natural solution to many more instrumental problems
than those to which it has already been applied.13
The camera has had
considerable application in astronomy, particularly meteor photography
and survey work of large star fields. It has been applied to stellar spectrographs,
and it is believed that it will have other applications in research where
extreme speed, a long spectral range, and a large field are important.
Two awkward features of the Schmidt camera are its curved focal plane
and the inaccessibility of the plate or film holder. The curvature of
the focal surface is R/2, where R is the radius of curvature
of the primary mirror. The focal surface is convex toward the sphere.

Fig.
41. |
The construction
of a Schmidt camera is so difficult that it should not be undertaken except
by one with considerable optical experience. The following is intended
primarily as a description of it.
The scheme of the
instrument is shown at the top of Fig. 41. It consists of a spherical
primary mirror and a Schmidt lens, which corrects the primary mirror for
spherical aberration. The lens is located at the center of curvature of
the spherical mirror, and its deviation from flatness is so small that
no great error of achromatism is produced by the dispersion of the index
of refraction of the glass from which it is made. However, as an optical
figuring job this deviation is great enough to make the construction of
the lens difficult. This is because the curve deviates as much from any
sphere as it does from flatness, so that all the construction difficulties
of making aspheric surfaces are encountered.
The Schmidt lens
may have several contours, as illustrated in Fig. 41. The variation of
thickness may be obtained by putting the curves entirely on one side of
the plate or on both sides. The variation in the thickness  of a plate of diameter 2r, expressed as a function of the distance
from the center of the plate y and the radius of curvature R
of the primary spherical mirror, can be represented by any one of the
family of curves
of a plate of diameter 2r, expressed as a function of the distance
from the center of the plate y and the radius of curvature R
of the primary spherical mirror, can be represented by any one of the
family of curves
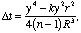
where k may
have any value between 0 and 4.
The characteristics
of some of the curves are as follows: Where k = 4, the lens is
too thick; where k = 0, the slope at the edge is so steep that
the construction difficulties are great; where k = 1.5, the achromatism
is best; where k= 1, the slopes are moderate, the color characteristics
are good, and the curve can be put half on one side of the plate and half
on the other. In the case where k = 1, the curve requires the least
glass to be removed.
The Schmidt lens
is made of Uviol glass or even fused quartz if the camera is to be used
for photography in the ultraviolet spectrum. The Schmidt camera has been
made to numerical apertures as fast as f/0.6. Such a camera is
much faster than a camera using a lens of corresponding aperture because
there are fewer glass surfaces to penetrate, and the light losses are
correspondingly less.

Fig. 42. |
The Schmidt plate
is ground and polished with a special ring tool. Each of the glass facets
for grinding or pitch facets for polishing is mounted on a separate spring
as in Fig. 42. This or a similar flexible construction of a tool is used
since considerable deformability is required of it.
The curve k
= 1 requires the thickness at the center to be the same as that at the
edge. This is indicated when a straightedge laid across the work will
touch the center but not rock on it. The minimum thickness of the plate
at y = 0.707r is determined from the thickness at the edge,
and the value of At calculated from the equation. The intermediary zone
is depressed by grinding until this minimum thickness corresponds with
that required as measured by a micrometer.
Figuring may be guided
by several testing schemes shown at the bottom of Fig. 28.
1 Ingalls,
Albert G., editor, Amateur Telescope Making, page 74. New York:
Scientific American Publishing Company, 1935.
2 For
a more comprehensive treatment of the theory of polishing from a different
point of view, see the following: Lord Rayleigh, Proc. Opt. Convention,
No. 1, page 73 (1905); and Scientific Papers, Vol. IV, page 542.
Cambridge: The University Press, 1903. French, J. W., "The Working of
Optical Parts," Dictionary of Applied Science, Vol. IV, page 326.
London: The Macmillan Company, 1923. Finch, G. I., "The Beilby Layer,"
Science Progress, 3l, 609 (1937).
3
I am indebted to Mr.
D. O. Eendrix for the procedures presented here.
4 Ingalls,
Albert G., editor, Amateur Telescope Making. New York: Scientific American
Publishing Company, 1935.
5 Diamond
glass cutters may be obtained from the Standard Diamond Tool Corporation,
64 West 48th Street, New York City. This company also sharpens diamond
glass cutters.
6 Topler,
A., Popp. Ann., 151, 33, 180 (1867). Wood, R. W., Ph7y&ical Optics,
page 93. New York: The Macmillm l Company, 1934.
7 Several
layers of the thin metal sheet are laid together on an anvil, and a sharp
needle is driven halfway through them. They are then separated and the
one with a suitable hole is selected. Each pierced sheet has a small hole
of a different size and all the holes are round.
8 See
article on Foucault's shadows by E. Gaviola, in Amateur Telescope Making,
Advanced (Albert G. Ingalls, editor), page 76. New York: Scientific
American Publishing Company, 1937.
9 Gaviola,
E., J.O.S.A., 26, 163 (1936).
10 Anderson,
J. A., and Porter, R. W., Astrophys. J., 70, 175 (1929).
11 For
further treatment of optical testing, see articles contained in Amateur
Telescope Making, Advanced, and references cited therein.
12 Brashear,
John A., Proc. of Am. Assn. for Adv. of Science, 38, 166 (1885).
13 Strömgren,
B., "Das Schmidtsche Spiegelteleskop," Vierteljahrschrift der Astronomischen
Gesellschaft, 70, 65 (1935). Smiley, C. H., "The Schmidt Camera,"
Popular Astronomy, 44, 415 (1936). |

![]()